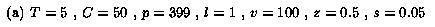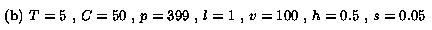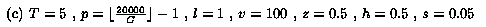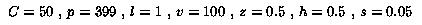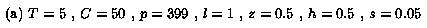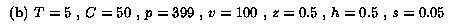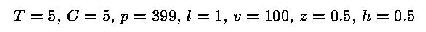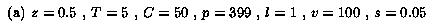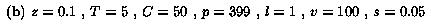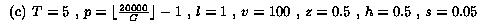NOSSDAV'01, June 25-26, 2001, Port Jefferson, New
York, USA.
Copyright 2001 ACM 1-58113-370-7/01/0006... $5.00.
The Utility of Feedback in Layered Multicast Congestion Control
Sergey Gorinsky and
Harrick Vin
Laboratory for Advanced Systems Research
Department of Computer Sciences
The University of Texas at Austin
Taylor Hall 2.124, Austin, TX 78712, USA
gorinsky@arl.wustl.edu,
vin@cs.utexas.edu
Abstract:
Layered multicast is a common approach for dissemination of audio and
video in heterogeneous network environments. Layered multicast schemes
can be classified into two categories - feedback-based and
feedback-free - depending on whether or not the scheme delivers
feedback to the sender of the multicast session. Advocates of
feedback-based schemes claim that feedback is necessary to match
the heterogeneous receiver capabilities efficiently. Supporters of
feedback-free schemes believe that feedback introduces significant
complexity and that a moderate amount of additional layers can balance
any benefit the feedback provides. Surprisingly, there has been no
systematic evaluation of these claims. This paper provides a
quantitative comparison of
feedback-based and feedback-free layered multicast schemes
with respect
to aligning the provided service to the capabilities
of heterogeneous receivers. We discover realistic scenarios when
feedback-free schemes require a very large number of
additional layers to match the performance of
feedback-based schemes. Our studies also demonstrate that
a light-weight feedback-based scheme can offer substantial
improvement in performance over feedback-free schemes
and can closely
approximate the efficiency achieved by the optimal feedback-based
scheme.
1. Introduction
Layered multicast has been suggested as a solution for real-time
dissemination of audio and video to heterogeneous receivers. In a
layered scheme, the sender encodes media content into a stack of
cumulative layers. The capability of a receiver determines which
layers it can receive.
Layered multicast schemes can be classified into two categories -
feedback-based and feedback-free. Feedback-based schemes measure the
receiver capabilities and communicate
them to the sender. Based on this feedback, the sender adjusts the
layer transmission rates to improve their alignment with the receiver
capabilities. SAMM (Source-Adaptive Multi-layered
Multicast) [16] and SIM
(multicast congestion control with Selective participation, Intra-group
transmission adjustment, and Menu adaptation) [6]
are examples of feedback-based schemes. Feedback-free schemes deliver
no feedback to the sender: the sender transmits the layers at
predetermined constant rates; the receivers indicate to the network
their desire to add or drop a layer by sending IGMP
(Internet Group Management Protocol) join or leave
messages [5], and, in response, routers modify their
multicast routing tables using such protocols as
DVMRP (Distance Vector Multicast Routing
Protocol) [17]. Examples of
feedback-free schemes include FLID (Fair Layered
Increase/Decrease) [2], RLM
(Receiver-driven Layered Multicast) [10], and RLC
(Receiver-driven Layered Congestion
control) [15].
While researchers have dedicated substantial efforts to the design of
specific schemes, it is not established which approach -
feedback-free or feedback-based - is preferable. As we discuss
below, each approach has its own advantages and drawbacks.
It has been shown that feedback-based schemes are better in
aligning the transmission rates of layers
to heterogeneous receiver capabilities.
Unfortunately, to achieve this efficiency, these schemes
introduce complexity of measuring and communicating the receiver
capabilities to the sender. In particular, to resolve the problem of
feedback implosion in large sessions, many feedback-based schemes use
routers or designated servers to aggregate feedback. This
infrastructure upgrade represents a detriment to the deployment of
such schemes. Also, the precise measurement of all the receiver
capabilities is difficult to realize in a heterogeneous multicast
session. The common method of probing for capacities (increase the
transmission if there is no congestion, decrease the transmission when
congestion is detected) does not reveal all the receiver capabilities
if the number of different capabilities exceeds the number of layers.
In addition, since the feedback-based schemes adjust the
transmission rates of the layers, the encoding process is more
complex.
The most appealing feature of feedback-free schemes
is their simplicity: to control congestion, receivers transmit only
IGMP messages. Since networks
have to support this type of control traffic in a scalable manner anyway
(for multicast routing), using
IGMP messages for
congestion control does not introduce additional complexity.
On the other hand,
feedback-free
schemes can suffer from a significant mismatch between the
statically allocated transmission rates and
the changing capabilities of heterogeneous receivers. Advocates of
feedback-free schemes argue that employing additional layers can
reduce this mismatch. However, by increasing the
number of layers, feedback-free schemes bring additional
complexity into encoding at the sender and decoding at the receivers
as well as raise the state and processing overhead in the routers (since these
schemes use a separate multicast group for each layer). Besides,
a larger number of layers affects adversely the compression
efficiency, and this increases the bandwidth required to provide the same
perceived quality.
The above arguments suggest that if feedback-free schemes would need
only a small number of additional layers to acquire the same level of
efficiency as given by feedback-based schemes, feedback-free schemes would
be preferable because of their simplicity.
Surprisingly, the literature
contains no quantitative assessment of such possibility.
In this paper, we compare feedback-based and feedback-free schemes
with respect to aligning the provided service to the
capabilities of heterogeneous receivers. We quantify the comparison
by measuring the additional number of layers required by feedback-free
schemes to achieve a comparable alignment.
Our studies reveal two realistic settings when
this layer overhead of feedback-free schemes can be large:
(1) the diversity of the receiver capabilities is smaller than
the bandwidth range useful for the multicast content, and (2) the
number of layers is roughly the same as
the number of different receiver capabilities. These findings
indicate tangible incentives for designing light-weight feedback-based
schemes. We describe one such scheme that communicates only a small
amount of information to the sender. Our experiments confirm that this light-weight
feedback-based scheme can offer substantial improvement in performance
over feedback-free schemes and can closely approximate the efficiency
delivered by the optimal feedback-based scheme.
The rest of the paper is organized as follows. Section 2
describes our model for bandwidth utility and receiver capabilities,
performance metrics, and compared schemes.
Section 3 explains the methodology, setup, and
results of our experiments. Section 4 introduces
and evaluates a light-weight feedback-based scheme.
Section 5 summarizes our conclusions and presents
directions for future research.
2. Model
We consider a session where a single sender multicasts content using
up to T cumulative layers. Let tk (such that
k = 0, ..., T-1)
denote the cumulative transmission rate for layer k. Similar
to earlier studies of layered multicast [12], we
represent these transmission rates tk with positive real
numbers. We assume that layer 0 is the base layer of the
hierarchical data encoding and that, for
k = 1, ..., T-1,
layer
k refers to the k-th enhancement layer of the encoding. That is,
we have
0 < t0 < t1 < ... < tT-1.
The receivers of the session are characterized by their
capabilities where the capability of a receiver is the maximum fair
rate at which the receiver can receive data from the sender.
The International Telecommunication Union (ITU) provides guidelines
for assessing the perceived quality of multimedia applications. For
example, ITU-R recommendation BT.500 defines the video quality scale
that ranges from 1 to 5: the value of 1 corresponds to a bad quality, 2
to poor, 3 to fair, 4 to good, and 5 to excellent [14].
Further, several studies have shown that while multimedia applications
need certain minimal amount of bandwidth to be practicable, the
marginal utility of additional bandwidth is negligible once the
perceived quality becomes excellent [1]. Based
on these studies, we represent the useful values of bandwidth as a
possible range [l, vl] where l is the lowest possible
capability (l > 0) and v is the
possible heterogeneity
(v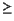 1). We assume that bandwidth smaller than l has no utility
for receivers and that bandwidth larger than vl does not increase the
utility. For bandwidth b that is between l and vl, we
characterize the bandwidth utility as a utility function u(b):
when b = l, utility u(b) equals 1, i.e., the perceived quality is
bad; as b grows to vl, utility u(b) increases to 5, i.e., to the
excellent quality.
We assume that receiver capabilities lie within the possible range -
receivers with capabilities below l do not benefit from receiving
data from the session; capabilities that exceed vl are equivalent to
vl in terms of their utility.
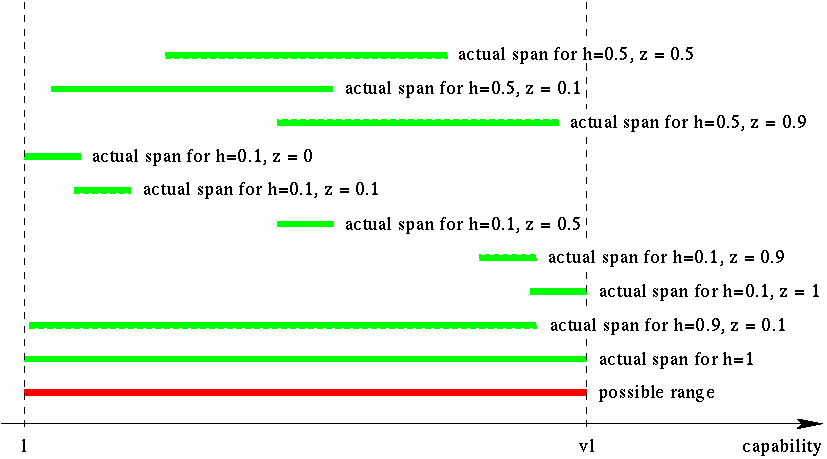
Note though that the size l(v-1) of the possible range can be
substantially larger than the actual span of receiver
capabilities: e.g., when all the receivers share the same bottleneck
link, their capabilities are identical. We characterize the actual
span with two parameters, size h and shift z, that take
their values between 0 and 1
(see Figure 1a):
1). We assume that bandwidth smaller than l has no utility
for receivers and that bandwidth larger than vl does not increase the
utility. For bandwidth b that is between l and vl, we
characterize the bandwidth utility as a utility function u(b):
when b = l, utility u(b) equals 1, i.e., the perceived quality is
bad; as b grows to vl, utility u(b) increases to 5, i.e., to the
excellent quality.
We assume that receiver capabilities lie within the possible range -
receivers with capabilities below l do not benefit from receiving
data from the session; capabilities that exceed vl are equivalent to
vl in terms of their utility.
Note though that the size l(v-1) of the possible range can be
substantially larger than the actual span of receiver
capabilities: e.g., when all the receivers share the same bottleneck
link, their capabilities are identical. We characterize the actual
span with two parameters, size h and shift z, that take
their values between 0 and 1
(see Figure 1a):
- Actual span size h refers to the percentage of the possible
range the actual span covers; h=1 when the actual span coincides
with the possible range [l, vl]; if h=0, all the receivers have
the same capability;
- Actual span shift z specifies the location of actual span
within the possible range [l, vl]. Formally, we define
z = x / ( (1 - h) (v - 1) l )
where x measures the gap between the lowest
possible capability l and the actual span while
(1-h)(v - 1)l is
the maximum value of this gap. For instance, z=0 when the lower
border of the actual span coincides with l; if z=0.5, the actual
span is in the middle of the possible range; when z=1, the upper
border of the actual span coincides with the highest possible
capability vl.
|
|
|
| (a) possible range and actual span |
| (b) capabilities within the actual span |
Figure 1:
Characterizing the receiver capabilities (click here to see an enlarged version). |
In reality, one could expect receiver capabilities to be
clustered around particular values rather than spread uniformly
throughout the actual span. There are two main reasons for such
expectations. First, when receivers share a bottleneck link, their
capabilities are the same.
Second, if the bottleneck link of a receiver is
its network access link, then the capability of this
receiver is likely to be slightly below the bandwidth of a
standard access technology such as 14.4 Kbaud, 28.8 Kbaud, 56 Kbaud
modem or 144 Kbps, 192 Kbps, 384 Kbps, 768 Kbps, 1.1 Mbps, 1.5 Mbps
DSL (Digital Subscriber Line).
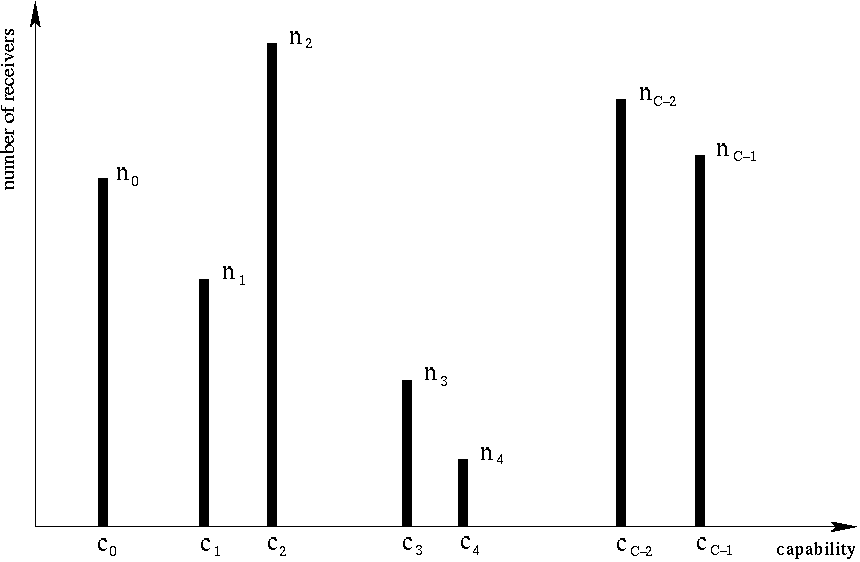
To model this clustered distribution of receiver capabilities, we
assume that the multicast session has n receivers with C different
receiver capabilities ci where C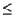 n
and
i = 0, ..., C-1.
We use ni to denote the number of receivers with capability ci
(see Figure 1b).
When evaluating the satisfaction of a receiver with the layered scheme,
we consider only those layers that do not create congestion.
We define an uncongested rate ri of a receiver with
capability ci as:
n
and
i = 0, ..., C-1.
We use ni to denote the number of receivers with capability ci
(see Figure 1b).
When evaluating the satisfaction of a receiver with the layered scheme,
we consider only those layers that do not create congestion.
We define an uncongested rate ri of a receiver with
capability ci as:
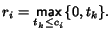 |
(1)
|
For example, if each layer adds 1 Mbps
to the total transmission rate, and the capability of a receiver
is 1.25 Mbps, then the receiver can obtain (without causing congestion)
only the base layer,
and this gives the receiver an uncongested rate of
1 Mbps. Since the receiver cannot obtain the enhancement layers
in their
entirety, they are not considered. In this respect,
the uncongested rate is similar to the ``goodput'' measure used in [16]
to represent the quality of layered video.
For a receiver with capability ci,
we quantify its satisfaction with the
transmission
rates by defining a receiver dissatisfaction di as:
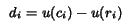 |
(2)
|
such that
di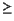 0.
Note that di = 0
when the layered scheme matches
the receiver capability
exactly. If the receiver does not receive even the base layer (i.e.,
ri = 0), then the dissatisfaction of this receiver is equal to
the utility of its capability:
di = u(ci).
Since we define
metric (2) as a difference of utilities, we can
interpret
the observed results in terms of
the standard scale for the perceived quality. For instance,
di = 1 means that the experienced quality is
one level worse (such as poor instead
of fair) than the receiver capability allows.
To assess the overall satisfaction of the session with the layered scheme, we
define a session dissatisfaction D as the average
of the receiver dissatisfaction
indices of all the receivers in the session:
0.
Note that di = 0
when the layered scheme matches
the receiver capability
exactly. If the receiver does not receive even the base layer (i.e.,
ri = 0), then the dissatisfaction of this receiver is equal to
the utility of its capability:
di = u(ci).
Since we define
metric (2) as a difference of utilities, we can
interpret
the observed results in terms of
the standard scale for the perceived quality. For instance,
di = 1 means that the experienced quality is
one level worse (such as poor instead
of fair) than the receiver capability allows.
To assess the overall satisfaction of the session with the layered scheme, we
define a session dissatisfaction D as the average
of the receiver dissatisfaction
indices of all the receivers in the session:
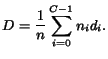
|
(3) |
Since feedback allows the sender to refine its estimates of the
receiver capabilities, it is reasonable
if a feedback-based scheme
yields a lower session dissatisfaction than a feedback-free scheme
with the same number of layers. The key question is how significantly
do these session dissatisfactions differ.
A good way to evaluate
the significance of the difference is to measure how many additional layers a
feedback-free scheme may need to have a comparable session dissatisfaction.
We formally define this additional
amount of layers as a layer overhead e:
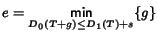 |
(4) |
where
D0(T+g) is the session dissatisfaction
for the feedback-free scheme with T+g layers, D1(T) denotes the session
dissatisfaction for the
feedback-based scheme with T layers, and s is a
satisfaction similarity characterizing
the closeness of the session dissatisfactions (s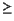 0;
note that
s = 0 when the feedback-free scheme has
at most the same dissatisfaction as the feedback-based scheme).
The fundamental difference between feedback-based and feedback-free schemes
is how much information about the receiver capabilities is available to
the sender. Unlike a feedback-based scheme, a feedback-free scheme
does not notify the sender about the actual capabilities of the
receivers. Thus, the sender of the
feedback-free scheme can rely only on a priori estimates of
the capabilities to set the transmission rates.
We assume that
the feedback-free sender knows only the possible
range [l, vl] of receiver capabilities and
selects the transmission rates to cover it.
In this paper, we examine
two feedback-free schemes suggested in the literature [2,15]:
0;
note that
s = 0 when the feedback-free scheme has
at most the same dissatisfaction as the feedback-based scheme).
The fundamental difference between feedback-based and feedback-free schemes
is how much information about the receiver capabilities is available to
the sender. Unlike a feedback-based scheme, a feedback-free scheme
does not notify the sender about the actual capabilities of the
receivers. Thus, the sender of the
feedback-free scheme can rely only on a priori estimates of
the capabilities to set the transmission rates.
We assume that
the feedback-free sender knows only the possible
range [l, vl] of receiver capabilities and
selects the transmission rates to cover it.
In this paper, we examine
two feedback-free schemes suggested in the literature [2,15]:
- Additive Layering (AL) scheme, where
each enhancement layer
increases the cumulative transmission rate by additive
 :
:
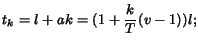 |
(5) |
- Multiplicative Layering (ML) scheme, where
enhancement layers
raise the cumulative transmission rate multiplicatively by factor
 :
:
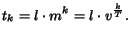 |
(6) |
Shacham [13]
provides a dynamic programming algorithm that,
given C, T, ci, and ni, computes an
optimal scheme with
respect to the session dissatisfaction.
We refer to this scheme
as an Optimal Layering (OL) scheme and use it as the
(best possible) representative of feedback-based schemes.
3. Experiments
Studies of adaptive video and audio applications show that the
marginal utility of bandwidth for such applications does not remain
constant: when the signal quality begins to be viable, the marginal
utility of extra bandwidth is substantial; as perceived quality
improves, the marginal utility of additional bandwidth
decreases [1,9]. However, evaluations
of layered multicast schemes commonly employ metrics - such as the
inter-receiver fairness [8] and reception
granularity [3] - that assume that the satisfaction of a
receiver grows linearly with the increase in the received rate. In
our experiments, we examine both of these utility functions (see
Figure 2):
- Linear utility
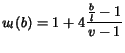 |
(7) |
that, as in the traditional evaluations of
layered multicast, increases linearly from
the bad quality to excellent, and
- Convex utility
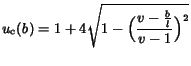 |
(8) |
that represents the case of the declining marginal utility
throughout the possible range.
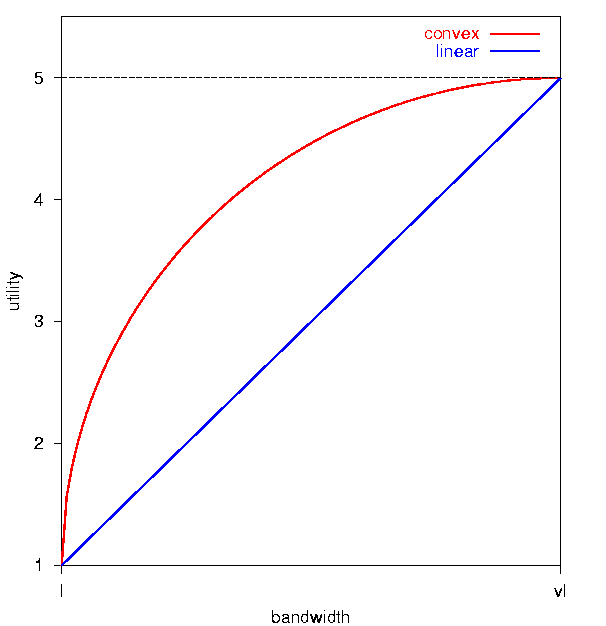 |
Figure 2:
Examined utility functions (click here to see an enlarged version). |
We pick the values of receiver capabilities ci within the actual
span randomly under the assumption of uniform distribution. Similarly,
we select the values of ni randomly, under the assumption of
uniform distribution, from interval [1, p] where p is the
maximum number of receivers with the same capability. While we claim
no special wisdom in instantiating our model for receiver
capabilities, we believe that our representation is more realistic
than those distributions that do not reflect the clustering of
receiver capabilities.
In our experiments, we explore all the dimensions in the parameter
space formed by our model: the maximum number of layers (parameter
T), the bandwidth range useful for the multicast content (parameters
l and v), the distribution of receiver capabilities (parameters
z, h, C, and p), and the acceptable satisfaction similarity
(parameter s). We observe how the choice of the bandwidth utility
function (linear versus convex) and the layering pattern (additive
versus multiplicative layering) affects the comparison of the
feedback-based and feedback-free schemes.
The default parameter settings in our experiments are as follows: T =
5 (the sender uses up to 5 layers), l = 1, v = 100 (the possible
range is [1, 100], this can correspond to the range of video rates
from 60 Kbps to 6 Mbps), z = 0.5, h = 0.5 (the actual span is in
the middle of the possible range and covers half of it), C = 50
(there are 50 different capabilities), p = 399 (the number of
receivers with a particular capability is picked randomly from
interval [1,399]; thus, the expected number of receivers is
(p+1)C/2=10000), and s = 0.05 (we measure how many
additional layers a feedback-free scheme needs to brings its session
dissatisfaction within 0.05 quality units from the session
dissatisfaction for the OL scheme).
When we vary a parameter, we consider a large number - 100 in most
of the experiments - of its settings distributed uniformly throughout
the examined range. For each considered setting, we generate 1000
session configurations (different due to the randomness in our
experimental setup) and compute the session dissatisfactions for the
OL, ML, and
AL schemes as well as the layer overheads for the
ML and AL schemes. We present the results
graphically as lines connecting the points that correspond to the
averages, over all the generated configurations, of the computed
values.
First, we examine how the location of the
receiver capabilities within the possible range impacts the
performance of the
OL, AL,
and ML schemes.
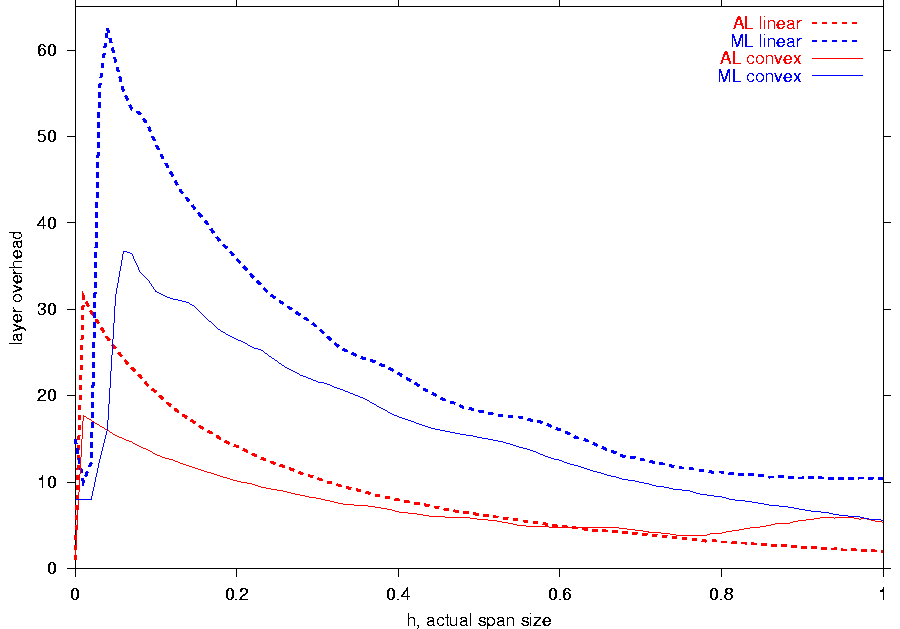
Figure 3a shows
that when the receiver capabilities are homogeneous
(i.e., for low
h), OL provides
an almost perfect satisfaction while AL
and ML need up to
60 additional layers to supply a comparable level of efficiency.
As h increases, the growing diversity
of the receiver capabilities drives the efficiency of
OL down,
and the layer overheads of AL
and ML converge to about 10 layers or below.

|
|
|
|
|
|
|
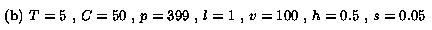
|
|
|
|
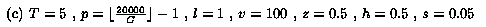
|
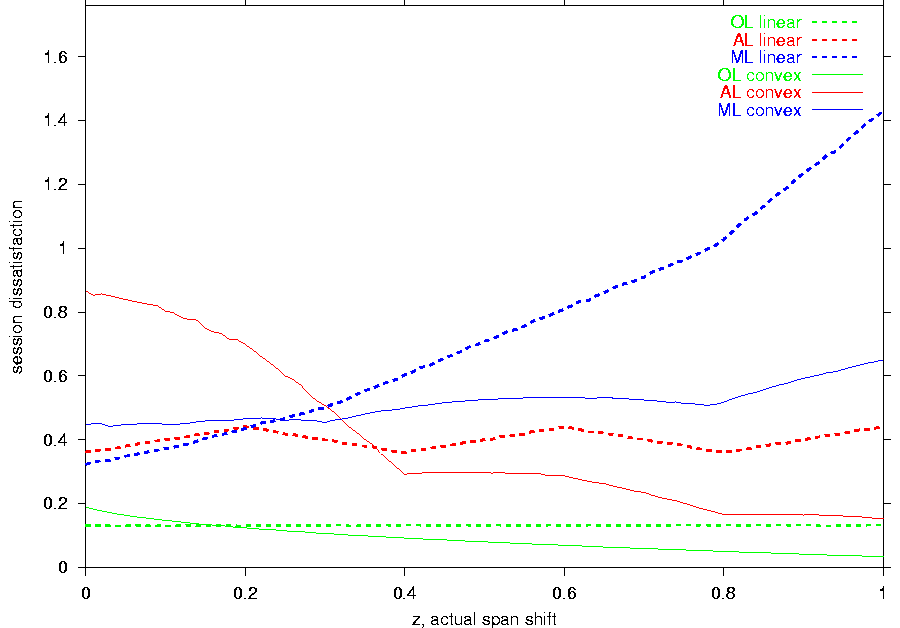
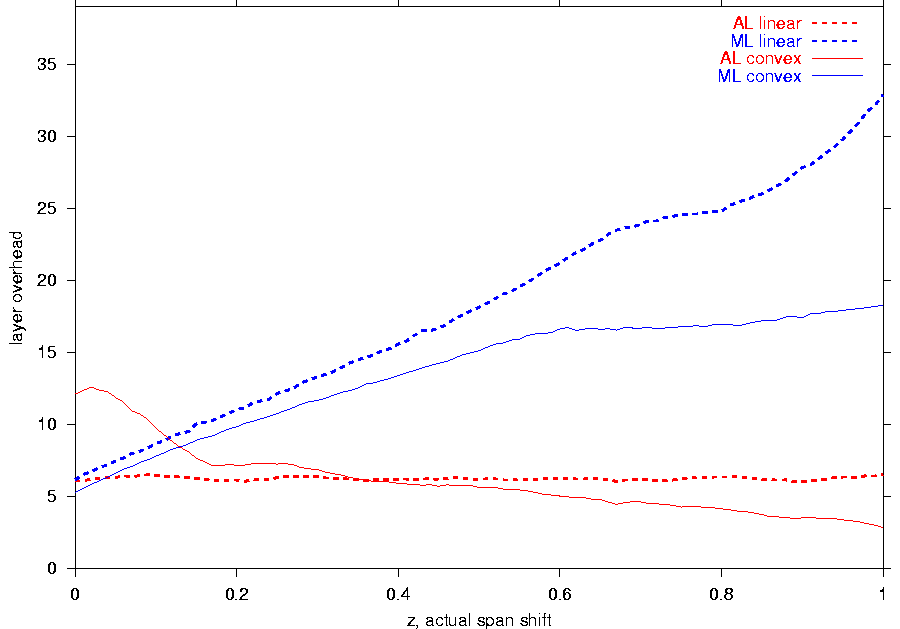
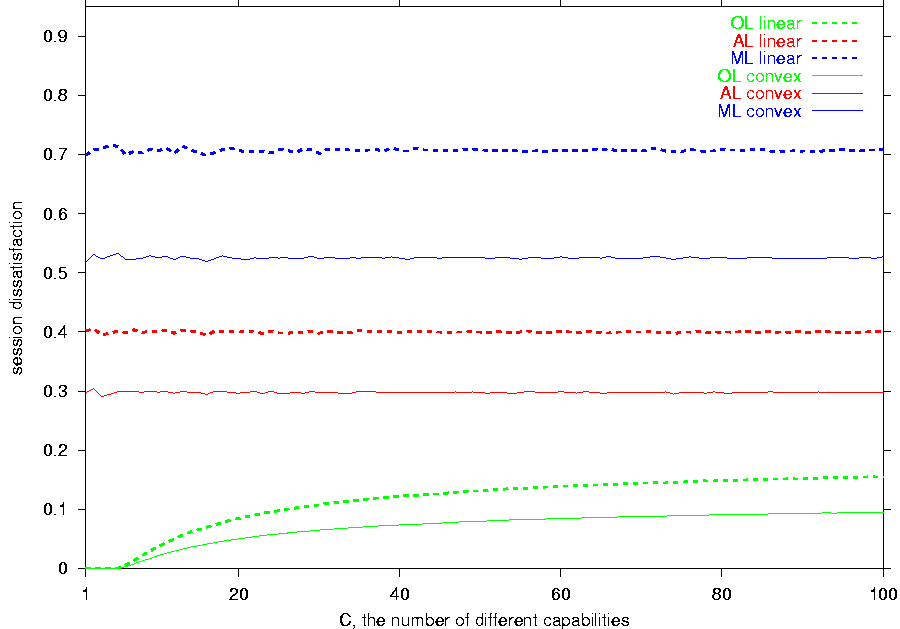
Figure 3:
The dependence on the: (a) actual span size, (b) actual span shift,
and (c) number of different capabilities (click here to see an enlarged version). |
A crucial observation for understanding the dependency on the
utility function is that for different functions, the same distribution
of the receiver capabilities
covers different spans on the utility scale.
Since z = 0.5 in the discussed experiment,
the actual span lies in the middle of
the possible range. Hence, when the actual span is small in comparison to
the possible range, the utility diversity of
the actual span is smaller for
the convex utility (see
Figure 2).
Consequently, all the examined schemes
achieve better performance
with the convex utility for low h.
When h is high, the utility diversities are similar for
the considered utility
functions, and
the placement of the transmission rates
becomes a more influential factor.
Since the convex function has much
larger marginal utility at low
capabilities, it gives much greater dissatisfaction
for the same difference in bandwidth
in the vicinity of l.
For AL with the convex
utility, the higher
dissatisfaction of less capable receivers
substantially outweighs
the lower dissatisfaction of more capable receivers.
Consequently, AL performs better with
the linear utility when h is large.
In comparison to AL, the
ML scheme places its rates
closer to l, and this allows ML to maintain
better performance with
the convex utility throughout the possible range.
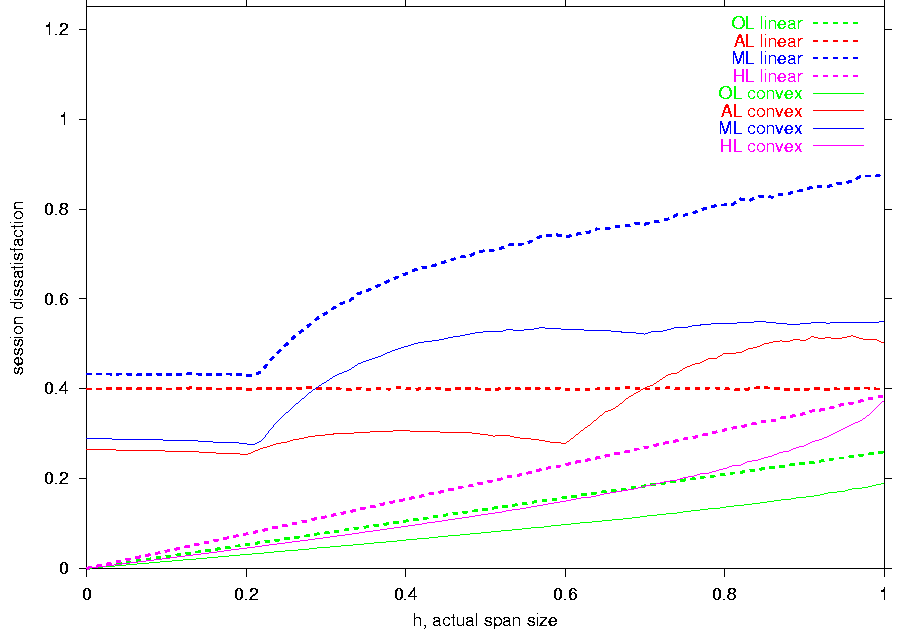
With increase of the actual span shift z (see Figure 3b),
the performance
balance between the feedback-free schemes flips: since AL,
in comparison to ML, sets its transmission rates
further from l, the ML scheme
outperforms AL
if z is low (i.e., when the receiver capabilities are closer
to l);
for larger z,
AL provides lower
dissatisfaction than ML.
A similar flipping pattern characterizes the dependence on the utility function.
Each of the three schemes achieves better performance
with the linear utility for low z and with the convex utility
for high z. Once again, the reason for such behavior lies with
the utility diversity of
the receiver capabilities: while the linear function yields a smaller
diversity when z is low, the convex function provides a smaller diversity
when z is large.
|
|
|
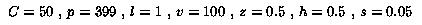
|
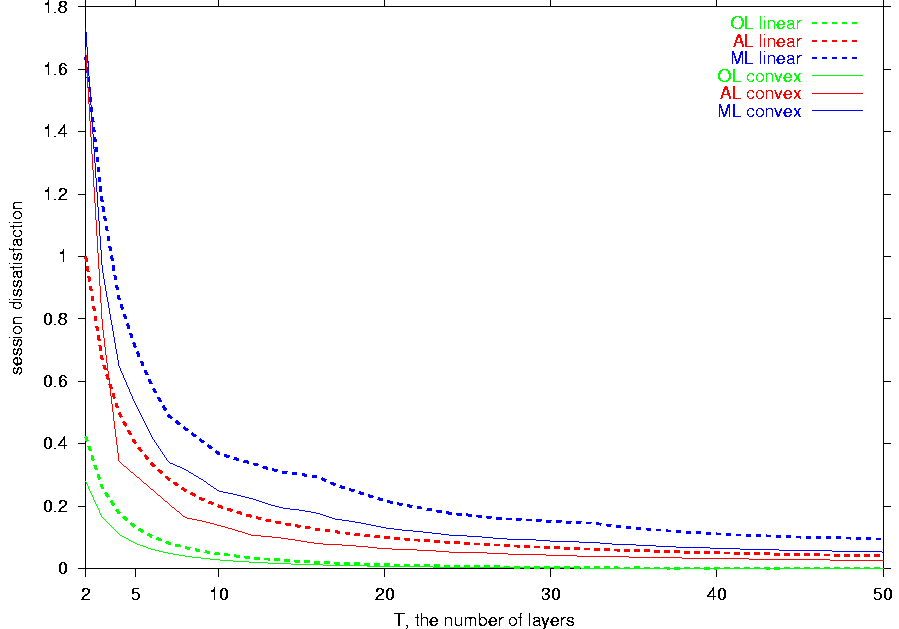
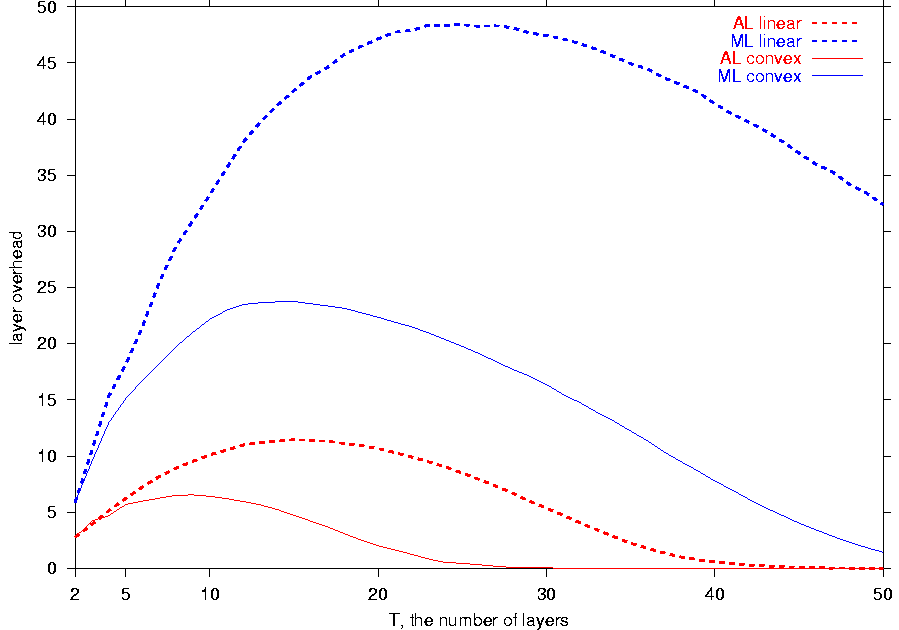
Figure 4:
The dependence on the number of layers (click here to see an enlarged version). |
|
|
|
|
|
|
|
|
Figure 5:
The dependence on the: (a) possible heterogeneity and (b) lowest possible capability
(click here to see an enlarged version). |
In Figure 3c, we vary C, the number of
different capabilities,
while keeping the expected number of receivers
close to 10000. Because changes in C do not alter
the utility diversities of the actual span,
the convex utility - which furnishes a smaller utility diversity
for the examined actual span -
gives lower dissatisfaction
to all the schemes and lower layer overhead to
both feedback-free
schemes.
When the number of different capabilities
is at most the number of layers, OL yields the 100%
satisfaction. For larger values of C,
the session dissatisfaction
for OL ascends while
the session dissatisfactions for AL
and ML remain on higher but
relatively constant levels.
Due to the declining efficiency of OL,
the
layer overhead for the feedback-free
schemes - which can be as large as 40 layers
when the number of layers and the number of
different
capabilities are roughly the same - reduces
as the
number of capabilities grows.
In contrast, as we observed by varying p while keeping C fixed
(we omit the corresponding graphs due to space constraints),
the number of receivers makes virtually no impact on the
performance of the OL, AL, and
ML schemes.
Figure 4 shows that as T, the number of layers, grows,
ML and AL fail to reach the same
satisfaction levels as provided by OL. Moreover,
as T increases up to 10 layers, the feedback-free schemes incur greater
layer overheads to provide comparable session dissatisfactions.
On the other hand,
less than 10 layers enable OL to bring the session
dissatisfaction
close to 0.
Since the utility diversity of the examined actual
span is lower with the convex function,
the convex utility provides ML and AL
with notably smaller dissatisfactions
and layer overheads for all but low values of T.
When T=2 or T=3, receivers that can receive only
the base layer rate of l are abundant. Because the
dissatisfaction of such receivers is much greater with the
convex function, the linear utility provides the feedback-free schemes
with better average performance when T is so low.
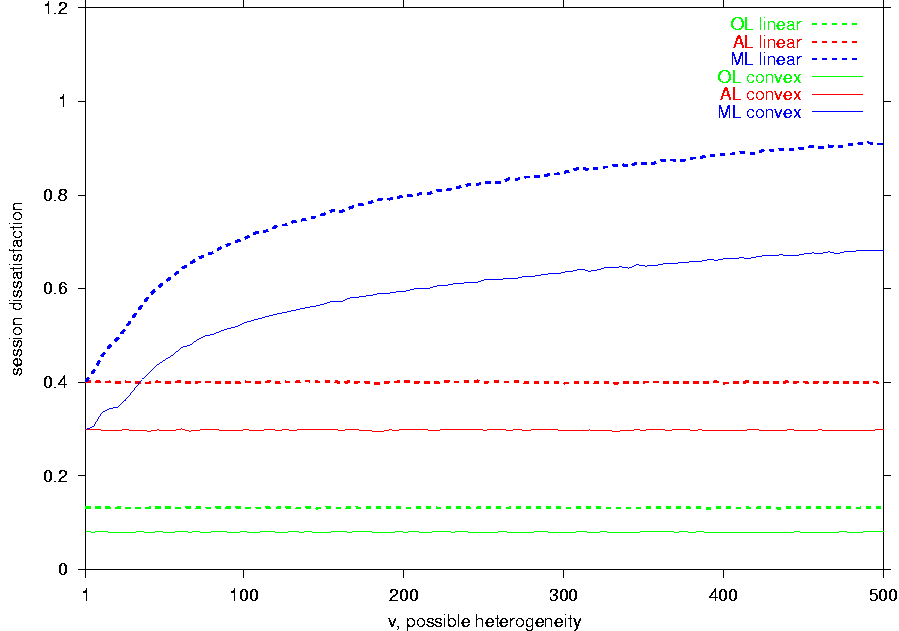
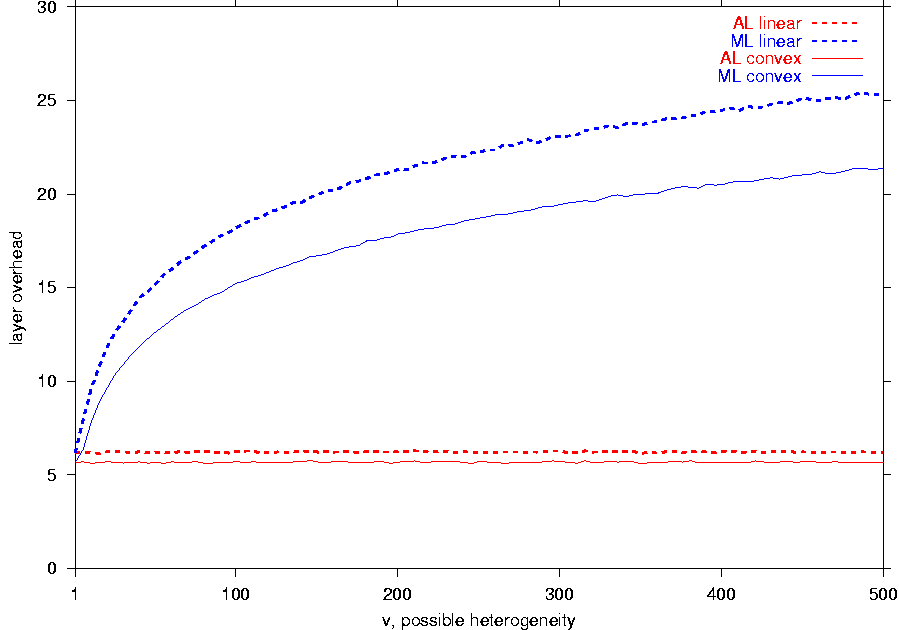
Figure 5a displays that
while the possible heterogeneity v does not change the performance
of the OL and AL schemes,
the session dissatisfaction and layer overhead of ML
grow as v increases. For the largest examined value v = 500,
the layer overheads of ML for the convex utility and
linear utility become around 22 and 26 layers respectively. However,
the layer overhead of AL remains at about 6 layers
for both utility functions.
The difference in the behaviors of the AL
and ML schemes can be explained as follows.
When the possible range increases, the actual span also expands so that
to stay in the middle of the possible range and cover half of it
(since z and h remain equal to 0.5).
The transmission rates of AL
also increase proportionally to spread uniformly throughout
the new possible range.
As a result, the relative positions of the actual span and the
transmission rates of AL do not change.
Consequently, the increase in v does not affect the performance of
the AL
scheme. On the other hand, as v grows,
the transmission rates of ML shift towards
l with respect to the
increasing actual span. In particular, more layers in ML
have cumulative transmission rates that are below the smallest
receiver capability, and also the number of the ML
transmission rates within the actual span decreases. Thus,
the performance of the ML scheme degrades as the possible
heterogeneity
increases.
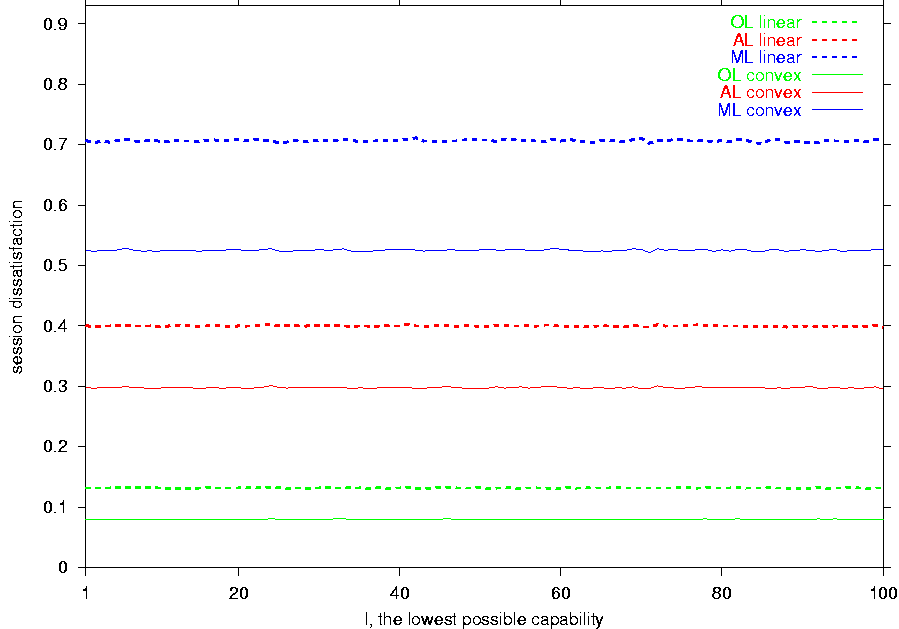
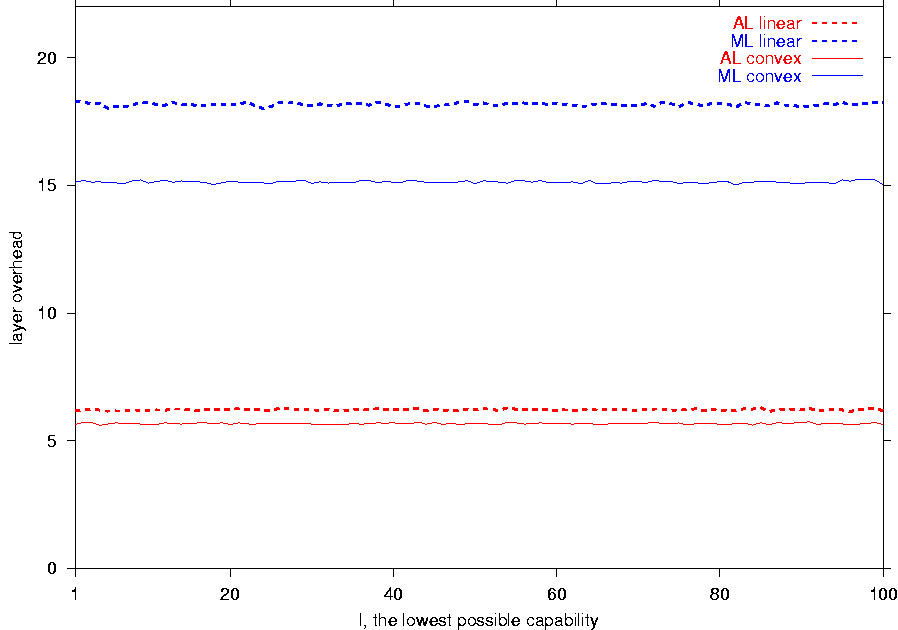
Figure 5b indicates
that the lowest possible
capability l does not affect
the performance of OL, AL,
and ML. This shows that
the units of capability measurements are irrelevant to the
comparison of the feedback-based and feedback-free schemes.
Figure 6 studies
the dependence of the layer overheads on the satisfaction
similarity s.
To bring the average session dissatisfaction within 0.2 quality units -
which constitute a substantial difference for audio and video
perception -
from the dissatisfaction of the OL scheme,
AL needs 4 additional layers with the linear utility
(or 2 additional layers with
the convex utility) while ML needs 10 and 5 additional layers
with the linear utility and convex utility respectively.
As s decreases, the layer overheads
grow exponentially.
To make their session dissatisfactions differ from the level of the
OL scheme by 0.01 quality units, the
AL and ML schemes
require more than 58 and 111 additional layers respectively.
Once again, because the utility diversity of the examined receiver capabilities
is lower with the convex function,
the convex utility provides AL and ML with
lower layer overheads for all values of s.
This section compared the feedback-based
OL scheme with the feedback-free AL
and ML schemes along all the dimensions in the parameter
space formed by our model. The distribution of
receiver capabilities was shown to affect the performance substantially.
We identified two major scenarios
where OL is
significantly superior to the feedback-free schemes:
(1) the receiver capabilities are homogeneous
in comparison to the bandwidth range useful for the
multicast content, and (2) the number of layers
and the number of different capabilities in the session are
on the same order of magnitude. While the number of different
capabilities is an
important parameter, the impact of the session size is
negligible.
Similarly, the location and size of
the possible range do not appear to influence the performance
of the examined schemes (except ML).
Somewhat surprisingly, additive layering consistently outperforms
multiplicative layering. The only exception takes place
when the receiver capabilities cluster closer
to the bottom of the possible range (i.e., for low z).
With respect to the bandwidth utility functions,
the convex utility commonly
provides lower session dissatisfaction
except in the cases of low z (for all the
schemes), extra low T (for the feedback-free schemes), and
high h (for the AL scheme).

|
|
Figure 6:
The impact of the satisfaction similarity (click here to see an enlarged version). |
4. Utility of Limited Feedback
Our findings reveal two realistic scenarios when layered multicast can
greatly benefit from information about the distribution of the
receiver capabilities: (1) the span of the capabilities is much
smaller than the bandwidth range useful for the multicast content, and
(2) the number of layers and the number of different capabilities
in the session are roughly the same. This indicates tangible
incentives for designing light-weight feedback-based schemes: if the
sender of a homogeneous session would learn the actual span of the
capabilities (a much easier task than discovering all the
capabilities), the session would need a much smaller number of layers
to achieve high satisfaction than if the sender knew only their
possible range. Thus, a successful approach can be a hybrid of the
feedback-free and feedback-based paradigms: feedback informs -
possibly at a coarse timescale - the sender about the lowest and
highest capabilities in the session, and the sender uses this range to
set - in the feedback-free fashion - the transmission rates of the
layers.
Below, we consider a Hybrid Layering scheme (HL)
that communicates the smallest receiver capability c0 and the
highest receiver capability
cC-1 to the sender of the session.
Using this information, the sender sets the cumulative transmission rates
tk of the HL scheme so that they grow additively by
(cC-1 - c0) / T per layer:
 |
(9) |
While the scalable communication of c0
and
cC-1 to
the sender is not a straightforward task (see [11]
for a possible approach), the sender in
HL needs to obtain only these two pieces of information
regardless of the session size. Thus, we conjecture that there is no
fundamental reason why the HL scheme could cause
feedback implosion and consequently should require feedback
aggregation.
In what follows, we compare the performance of HL
with the already examined OL, AL,
and ML schemes in the two major scenarios when the
feedback-free schemes incur substantial layer overhead.
To assess the performance of HL in the case of
homogeneous receiver capabilities, we repeat the experiment from
Figure 3a for the OL,
AL, ML, and HL schemes.
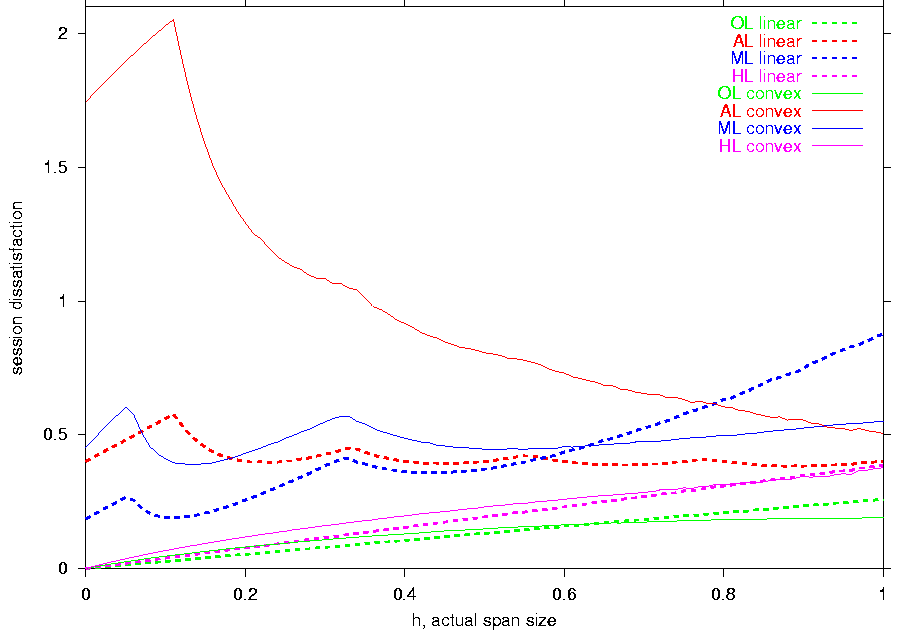
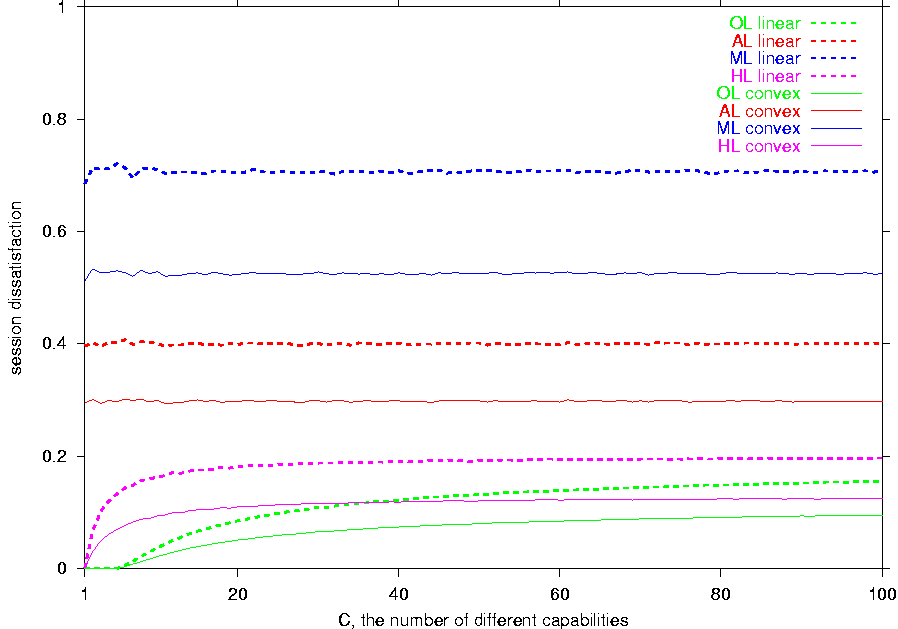
Figure 7a shows that HL offers a
dramatic improvement in dissatisfaction and layer overhead over the
feedback-free schemes when h is small, i.e., when the feedback-free
schemes are the most inefficient. Moreover, the session
dissatisfaction of HL remains close to the level
provided by the optimal scheme OL. Consequently, the
layer overhead of this hybrid scheme is low: for small values of h,
the layer overhead of HL is negligible; as the
receiver capabilities spread to cover the possible range (when h
=1), the overhead increases but still stays below 3 layers. Hence,
HL extracts a great benefit from the limited
feedback of just two values c0
and
cC-1. The
utility of communicating the rest of the receiver capabilities to the
sender is significantly lower.
According to the comparison of the feedback-free schemes in
Section 3, additive layering consistently
outperforms multiplicative layering except when z is small. Since
the examined HL scheme sets its transmission rates
in the additive fashion, it is interesting to check whether this
feature undermines the efficiency of HL when z is
low. Figure 7b repeats the experiment from
Figure 7a for z=0.1 and demonstrates that
HL preserves its superior performance in comparison to both
the AL and ML
schemes. Furthermore, the HL scheme still needs only
a few of additional layers to make its session dissatisfaction
comparable to the one provided by the optimal feedback-based scheme.
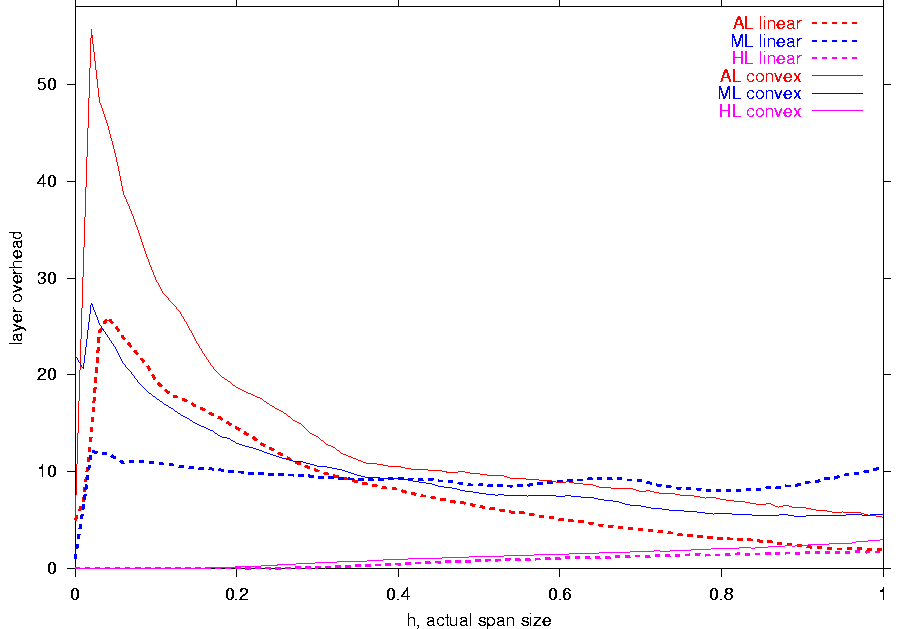
To evaluate the performance of HL in the second
major disadvantageous case for the feedback-free schemes (i.e., when
the number of layers and the number of different capabilities are
roughly the same), we repeat the experiment from
Figure 3c with the OL,
AL, ML, and HL schemes and
report the results in Figure 7c.
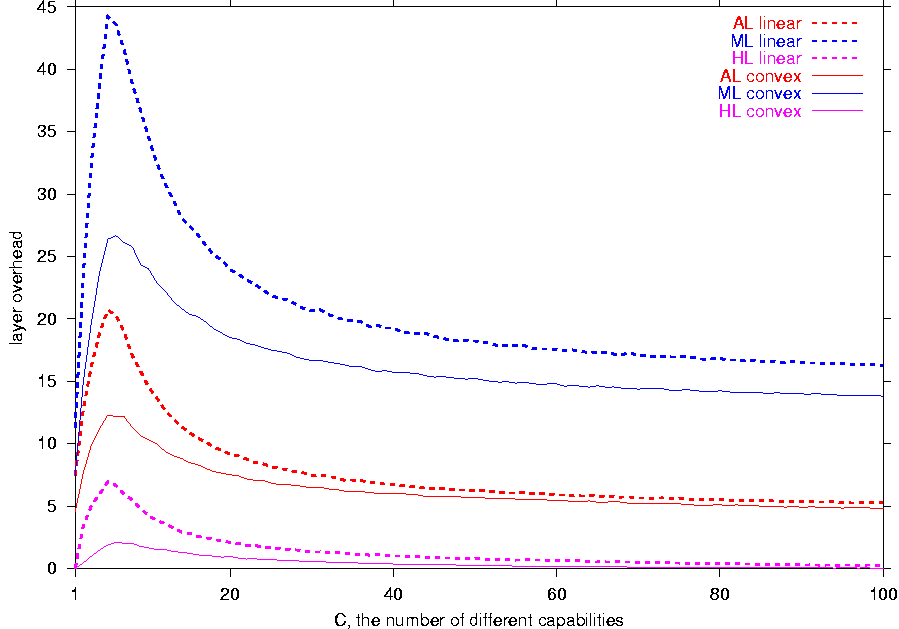
Once again, HL performs much better than the AL and
ML schemes. For the linear utility function, the
peak layer overheads for the ML,
AL, and HL schemes are 44, 21, and 7 additional
layers respectively. For the convex utility, the maximum overheads for
ML, AL, and HL
are 27, 12, and 2 layers respectively. While the HL
scheme greatly outperforms the feedback-free schemes,
Figure 7c
indicates opportunities for further
improvement. It is possible that different light-weight schemes with a
small amount of feedback information (such as the top T most common
receiver capabilities inferred from the multicast tree
topology [7])
can provide even better performance.
|
|

|
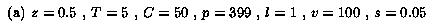
|
|
|
|
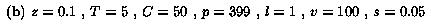
|
|
|
|
|
Figure 7:
The assessment of the hybrid scheme HL
(click here to see an enlarged version). |
5. Concluding Remarks
This paper compared feedback-free and feedback-based layered multicast schemes
with respect to aligning the
provided service to the capabilities of heterogeneous receivers.
We discovered several realistic scenarios when
feedback-free schemes require a very large number of
additional layers to match the performance of
feedback-based schemes. We also demonstrated that
a light-weight feedback-based scheme can offer substantial
improvement in performance over feedback-free schemes
and can closely
approximate the efficiency delivered by the optimal feedback-based
scheme.
We envision two main directions for future
work. Section 5.1 discusses how to make our current
model more realistic. Sections 5.2 and 5.3
outline two aspects of layered multicast that are, in our opinion,
important but routinely ignored by proposed multicast designs.
5.1 Model Refinements
To compare the feedback-based and feedback-free schemes, we used
the layer overhead as a chief metric. However, our
current model does not reflect two factors that can substantially
increase the number of additional layers needed by a feedback-free
scheme to compensate for the lack of feedback. First, a larger number
of layers usually leads to a smaller compression ratio. Accounting for
the declining compression ratio not only can raise the layer overhead
but also is likely to reveal scenarios when additional layers cease to
improve satisfaction (i.e., when the layer overhead is infinite).
Another relevant issue with feedback-free congestion control is its
responsiveness: after the last subscriber of a session in a subnet
sends an IGMP leave message, up to 10 seconds can
elapse before the last-hop router stops forwarding the session traffic
into the subnet. The feedback-free technique of dynamic
layering [2] tackles this problem of responsiveness but
at the price of even further increase in the number of additional
layers.
We plan to adjust our model to represent the dependencies on the
compression ratio and control responsiveness.
5.2 The First-Hop Problem
To control congestion, feedback-free schemes adjust multicast routing
tables. Therefore, a feedback-free scheme cannot resolve congestion if
it occurs on the first hop between the sender and the top router in
the multicast tree of the session. The sender keeps transmitting all
the layers into the network regardless of the congestion and the
receiver capabilities. Even if the session has no subscribed receivers,
the sender can keep sending its packets which are discarded by
the first router. This first-hop problem can manifest itself as
unfair sharing of bandwidth or even as congestion
collapse.
In future, we will assess the severity of the first-hop problem and
work on possible solutions. It appears that to be safe for deployment
in the Internet, feedback-free layered
multicast protocols should be made end-to-end by propagating the
layer subscription information all the way to the sender. This approach,
however, requires changes in the network infrastructure
and brings additional complexity.
5.3 Trust and Privacy
While it has been argued that multicast congestion control should not
assume trust and cooperation among receivers [4],
existing congestion control designs for
multicast commonly ignore the issues of distrust and privacy. Since
receivers are the only entities regulating congestion in feedback-free
schemes, these schemes seem to be more vulnerable in the presence of
misbehaving receivers. Including the sender into the
congestion control loop can
protect against the threats posed by some types of receiver misbehavior.
We are investigating whether the feedback-based
approach to layered multicast
can ensure better performance in a distrusted network
environment.
- 1
-
L. Breslau and S. Shenker.
Best-Effort versus Reservations: A Simple Comparative Analysis.
In Proceedings ACM SIGCOMM'98, September 1998.
- 2
-
J. Byers, M. Frumin, G. Horn, M. Luby, M. Mitzenmacher, A. Roetter, and
W. Shaver.
FLID-DL: Congestion Control for Layered Multicast.
In Proceedings NGC 2000, November 2000.
- 3
-
J. Byers, M. Luby, and M. Mitzenmacher.
Fine-Grained Layered Multicast.
In Proceedings IEEE INFOCOM 2001, April 2001.
- 4
-
N.G. Duffield, M. Grossglauser, and K.K. Ramakrishnan.
Distrust and Privacy: Axioms for Multicast Congestion Control.
In Proceedings NOSSDAV'99, June 1999.
- 5
-
W. Fenner.
Internet Group Management Protocol, Version 2.
RFC 2236, November 1997.
- 6
-
S. Gorinsky, K.K. Ramakrishnan, and H. Vin.
Addressing Heterogeneity and Scalability in Layered Multicast
Congestion Control.
Technical Report TR2000-31, Department of Computer Sciences, The
University of Texas at Austin, November 2000.
- 7
-
S. Jagannathan, K. Almeroth, and A. Acharya.
Topology Sensitive Congestion Control for Real-Time Multicast.
In Proceedings NOSSDAV 2000, June 2000.
- 8
-
T. Jiang, E. W. Zegura, and M. H. Ammar.
Inter-Receiver Fairness: A Novel Performance Measure for Multicast
ABR Sessions.
In Proceedings ACM SIGMETRICS'98, June 1998.
- 9
-
J. Kimura, F.A. Tobagi, J. Pulido, and P.J. Emstad.
Perceived Quality and Bandwidth Characterization of Layered MPEG-2
Video Encoding.
In Proceedings of the SPIE International Symposium on Voice,
Video and Data Communications, September 1999.
- 10
-
S. McCanne, V. Jacobson, and M. Vetterli.
Receiver-driven Layered Multicast.
In Proceedings ACM SIGCOMM'96, August 1996.
- 11
-
L. Rizzo.
pgmcc: A TCP-friendly Single-Rate Multicast Congestion Control
Scheme.
In Proceedings ACM SIGCOMM 2000, August 2000.
- 12
-
D. Rubenstein, J. Kurose, and D. Towsley.
The Impact of Multicast Layering on Network Fairness.
In Proceedings ACM SIGCOMM'99, September 1999.
- 13
-
N. Shacham.
Multipoint Communication by Hierarchically Encoded Data.
In Proceedings IEEE INFOCOM'92, May 1992.
- 14
-
International Telecommunication Union.
Methodology for the Subjective Assessment of the Quality of
Television Pictures.
ITU-R Recommendation BT.500-10, March 2000.
- 15
-
L. Vicisano, L. Rizzo, and J. Crowcroft.
TCP-like Congestion Control for Layered Multicast Data Transfer.
In Proceedings IEEE INFOCOM'98, March 1998.
- 16
-
B. Vickers, C. Albuquerque, and T. Suda.
Source-Adaptive Multi-Layered Multicast Algorithms for Real-Time
Video Distribution.
IEEE/ACM Transactions on Networking, December 2000.
- 17
-
D. Waitzman, C. Partridge, and S. Deering.
Distance Vector Multicast Routing Protocol.
RFC 1075, November 1988.



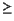 1). We assume that bandwidth smaller than l has no utility
for receivers and that bandwidth larger than vl does not increase the
utility. For bandwidth b that is between l and vl, we
characterize the bandwidth utility as a utility function u(b):
when b = l, utility u(b) equals 1, i.e., the perceived quality is
bad; as b grows to vl, utility u(b) increases to 5, i.e., to the
excellent quality.
1). We assume that bandwidth smaller than l has no utility
for receivers and that bandwidth larger than vl does not increase the
utility. For bandwidth b that is between l and vl, we
characterize the bandwidth utility as a utility function u(b):
when b = l, utility u(b) equals 1, i.e., the perceived quality is
bad; as b grows to vl, utility u(b) increases to 5, i.e., to the
excellent quality.


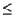 n
and
i = 0, ..., C-1.
We use ni to denote the number of receivers with capability ci
(see Figure 1b).
n
and
i = 0, ..., C-1.
We use ni to denote the number of receivers with capability ci
(see Figure 1b).
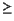 0.
Note that di = 0
when the layered scheme matches
the receiver capability
exactly. If the receiver does not receive even the base layer (i.e.,
ri = 0), then the dissatisfaction of this receiver is equal to
the utility of its capability:
di = u(ci).
Since we define
metric (2) as a difference of utilities, we can
interpret
the observed results in terms of
the standard scale for the perceived quality. For instance,
di = 1 means that the experienced quality is
one level worse (such as poor instead
of fair) than the receiver capability allows.
To assess the overall satisfaction of the session with the layered scheme, we
define a session dissatisfaction D as the average
of the receiver dissatisfaction
indices of all the receivers in the session:
Since feedback allows the sender to refine its estimates of the
receiver capabilities, it is reasonable
if a feedback-based scheme
yields a lower session dissatisfaction than a feedback-free scheme
with the same number of layers. The key question is how significantly
do these session dissatisfactions differ.
A good way to evaluate
the significance of the difference is to measure how many additional layers a
feedback-free scheme may need to have a comparable session dissatisfaction.
We formally define this additional
amount of layers as a layer overhead e:
0.
Note that di = 0
when the layered scheme matches
the receiver capability
exactly. If the receiver does not receive even the base layer (i.e.,
ri = 0), then the dissatisfaction of this receiver is equal to
the utility of its capability:
di = u(ci).
Since we define
metric (2) as a difference of utilities, we can
interpret
the observed results in terms of
the standard scale for the perceived quality. For instance,
di = 1 means that the experienced quality is
one level worse (such as poor instead
of fair) than the receiver capability allows.
To assess the overall satisfaction of the session with the layered scheme, we
define a session dissatisfaction D as the average
of the receiver dissatisfaction
indices of all the receivers in the session:
Since feedback allows the sender to refine its estimates of the
receiver capabilities, it is reasonable
if a feedback-based scheme
yields a lower session dissatisfaction than a feedback-free scheme
with the same number of layers. The key question is how significantly
do these session dissatisfactions differ.
A good way to evaluate
the significance of the difference is to measure how many additional layers a
feedback-free scheme may need to have a comparable session dissatisfaction.
We formally define this additional
amount of layers as a layer overhead e:
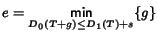
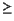 0;
note that
s = 0 when the feedback-free scheme has
at most the same dissatisfaction as the feedback-based scheme).
0;
note that
s = 0 when the feedback-free scheme has
at most the same dissatisfaction as the feedback-based scheme).